插入排序(Insertion Sort)是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入,插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位的过程,为实现算法的高效,本算法中使用了一个结构体元素来保存数据和其对应的索引。
下面是插入排序的Python实现:
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
arr = [12, 11, 13, 5, 6]
insertion_sort(arr)
print("排序后的数组:")
for i in range(len(arr)):
print("%d" % arr[i], end=" ")
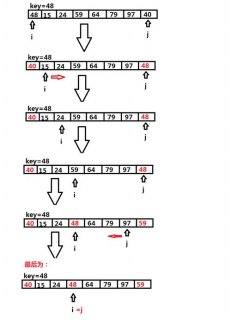
在这个实现中,我们首先遍历数组中的每个元素(从第二个元素开始),将其作为待插入元素,我们将这个元素与前面的元素进行比较,如果当前元素小于前面的元素,则将前面的元素后移一位,直到找到合适的位置插入当前元素,经过一次遍历,数组就变成了有序序列,我们需要对整个数组进行n-1次遍历,其中n为数组的长度。
插入排序的时间复杂度为O(n^2),在最坏情况下(即输入数据完全逆序时),时间复杂度为O(n^2),虽然插入排序的时间复杂度较高,但它在小规模数据或者部分有序数据上表现较好,插入排序的空间复杂度为O(1),因为它不需要额外的空间来存储数据。
相关问题与解答:
1. 与冒泡排序相比,插入排序的优势是什么?

答:与冒泡排序相比,插入排序的优势在于其空间复杂度较低(O(1)),并且在部分有序的数据上表现较好,插入排序的时间复杂度较高(O(n^2)),在处理大规模数据时可能效率较低。
2. 如何优化插入排序算法?

 微信扫一扫打赏
微信扫一扫打赏



电脑配置配的什么呀,真是令人眼前一亮,独特的见解让人耳目一新,友好评论更是让人感受到你的诚意。
组装电脑玩dnf,建议配备高性能处理器和显卡,确保流畅运行,选择大容量内存和高速固态硬盘,提升游戏体验,注意散热和电源稳定性,祝你玩得愉快!
在冬天组装电脑,应特别注意防静电和保持室内温暖,选择适合低温环境的优质配件,细心操作,不仅可以确保电脑的正常运行,还能在寒冷中享受科技带来的温暖。
组装主机需按需配置,平衡性能与价格,优先考虑散热与稳定性。
8千电脑的配置通常能满足大部分用户的需求,但具体配置要根据个人使用习惯和场景来选择,建议关注处理器、内存、硬盘和显卡等关键部件,同时也要考虑售后服务和保修政策,